Why is the snap logo a lambda?λλλλλλ Why? Please tell me why.
Ah. You are about to enter the mysteries of the real way in which Snap! is better than Scratch. (Not that we're better in all ways!)
So, first you have to understand about first class data types. A data type is first class in a language if its instances can be
- The value of a variable.
- An input to a procedure.
- The returned value from a procedure.
- A member of an aggregate (in our case, that means a list).
- in existence without having a name.
So, we start with the easier of the two big things we added to Scratch: first class lists.
In Scratch, if you want a list, you click Make a List, and you have to give it a name. That's not exactly the same as being the value of a variable, because there's nothing like SET for list names. Its name can only ever name this list once you've made it. But we'll be generous and say that's close enough.
But what about the others? Can a list be the input to a procedure? That is, can you say
![]() ? Nope. (Or rather, you can, but you get a text string, not the list.)
? Nope. (Or rather, you can, but you get a text string, not the list.)
And can a reporter report a list? Is there anything like
And can you put a list as an item in another list? No.
And you can't make a list without giving it a name.
So, one of the big differences between Snap! and Scratch is that we have first class lists and they don't.
Okay, now that you understand that, we're ready to talk about (drumroll please) first class procedures. A picture being worth 1000 words, here's my standard opening example:
![]()

You click on 2+3 and you get 5, just as you'd expect. But if you put the 2+3 inside a gray ring (most easily done by right-clicking and choosing "ringify"), then the value of the expression is the procedure itself. The gray ring is our visual representation of lambda.
The ring creates an anonymous procedure. And they're first class:

... and so on.
So now, to answer your question, this idea of function as data was invented in umm the 1930s? '40s? by Alonzo Church, a mathematician, who used the lambda to denote a function, like this:
λx . x+3
for the function that adds 3 to its input.
Then when John McCarthy invented Lisp in 1962, he took inspiration from Church's "lambda calculus" and denoted functions as
(lambda (x) (+ x 3))
Starting right then in 1962 and continuing to this day, Real Programmers (← sarcasm, in case you can't tell, but not my invention; everyone knows what you mean when you say it) have declared Lisp to be a useless piece of ivory tower thinking that has no serious purpose, because it's too slow for practical use. But in the intervening time, one by one, the "impractical" ideas from Lisp have been adopted by every other major language. The big jump came when they put a garbage collector in Java. But now even C++ has lambda. And functions as data are at the heart of Snap!.
P.S. I haven't explained why this is a useful idea. But this is enough for tonight; I don't want your head to explode.
Lambda is the mechanism through which we create anonymous functions. Sometimes we then give the functions a name. For example, if you read the code of the sort block in the list utilities library, which uses mergesort, since we don't (yet) have an internal definition mechanism, it creates helper functions with things like SET (MERGE) TO (stuff in a ring). And then in the main body we say (CALL MERGE WITH INPUTS ...). Sometimes it's really important that the function-creation mechanism captures the environment in which the new function is created. The classic example:
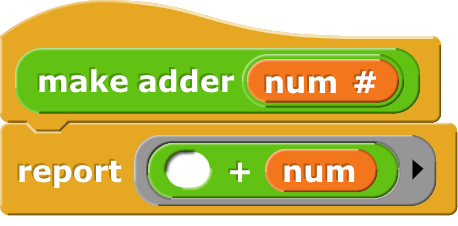
This uses our amazing feature that lets beginners use higher order functions without really thinking about functions at all, by using an empty input slot as an implicit formal parameter. But if you want it to look like a classic lambda expression, we can do that too:
And then, either way:

The point of the example is that add3 and add5 have the same body (x+num), so if they behave differently it must be because each remembers what value num had when it was created.
The great thing about lambda calculus is that Church showed how, starting with nothing but lambda and CALL, you can carry out any computation. No variables other than the parameters of lambda expressions, no arithmetic, no lists, just lambda and call. Very cool.



